Paper-Analysis-Exploring Extreme Parameter Compression for Pre-trained Language Models

Title and Authors

Exploring Extreme Parameter Compression for Pre-trained Language Models

Background and Motivation

Pre-trained language（Bert and ALbert）大规模PLM的部署是具有挑战性的

1. 模型不能完全部署或存储在单个GPU服务器中，模型并行性将消耗许多服务器之间的网络通信的额外时间；
2. 边缘设备可能没有足够的空间来存储模型；
3. 长的推理时间无法支持实时反馈

PLM中的参数冗余可以分成两类：

• intra-matrix redundancy。常发生在可以分开计算的heads中，头部之间的注意力作用于相似的子空间，因此是低秩的，同时每个FFN层都可以分解为许多独立的子FFN
• inter-matrix redundancy。发生在不同的层之间，例如，层之间的注意力图可能相似。

对Transformer层中的主要权重矩阵的探索发现，这些权重矩阵可以以低秩的方式进行近似——证明了可能的矩阵内冗余和矩阵间冗余。本文分析比较了用于参数压缩的不同分解方法，包括矩阵分解，tt分解和tucker分解。区别在于

• 由于intra-matrix冗余而对每个权重矩阵进行矩阵分解
• 对于inter-matrix冗余，tt分解共享head和tail矩阵同时保持core matrix冗余
• tucker分解引入matrix bank，使得parameter scale几乎恒定
  得出的结论是就压缩比而言，tucker分解比其他分解更有效。matrix/tensor 分解面临的挑战为
• 分解可能导致原始权重和近似权重之间的差异，并且在大压缩比的情况下不可能进行精确分解。相反，知识蒸馏以损失感知的方式模拟原始模型的预测
• 其次，重建可能导致额外的计算成本。有效的重建协议是通过对乘法运算进行重新排序来实现的，这些乘法运算也保持了相同的结果。

Main Contributions

这项工作的贡献是：

1. 我们提出了一个具有标准化术语的形式化框架，以全面讨论矩阵/张量分解方法来压缩基于Transformer的语言模型；
2. 我们采用张量分解来压缩PLM，这也更快，而现有的工作没有显示出PLM加速的潜力；
3. 我们的压缩BERT在Transformer层中具有1/7个参数，其性能与GLUE基准测试中的原始BERT相当。此外，一个微小的版本在Transformer中仅具有1/48个参数，实现了96.7%的BERT基础性能，推理速度快2.7倍。我们直接在TinyBERT上使用所提出的方法（Jiao et al.，2020），该方法纯粹基于KD，因为我们的工作是对KD等现有压缩方法的补充。

Related Work

Compressing PLMs. 本文专注于基于transformer的预训练语言模型的压缩，而不是设计新的transformer。本文重用现有的模型，现有的压缩方法有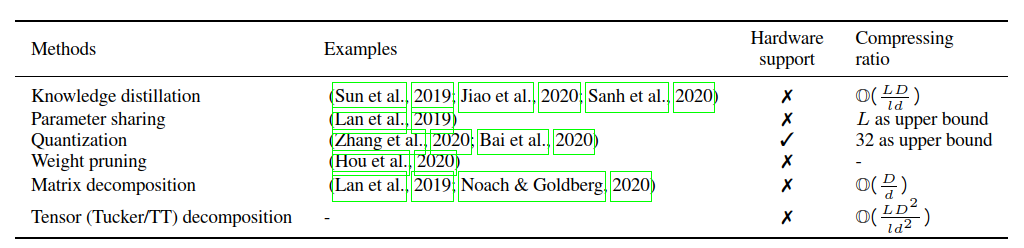

我们认为，现有的压缩方法（见表1）可能不足以进行极端参数压缩，这一点正在研究中。原因是多方面的，首先，基于知识提取的方法通常从头开始学习新的学生模型，在提取之前不能从教师模型继承太多知识。其次，一些方法具有压缩比的上限。例如，层共享ALBERT以最大L次压缩共享L层中的参数。量化将现有的32位参数替换为最大减少32倍的二进制参数。此外，量化还需要进一步的硬件支持，这通常是针对特定平台的。可以说，重量修剪不能实现大的压缩比。

matrix/tensor decomposition for compression 我们认为，使用矩阵/张量分解的现有工作的压缩比的PLM相对较小；它们中的大多数不具有加速效应，限制了它们在大规模PLM中的应用。利用矩阵/张量分解压缩PLM的潜力正在研究之中。在这项工作中，我们采用张量分解，对PLM的参数进行三次压缩。

Theoretical Framework/Algorithm

PLM本质上是多个transformer的堆叠.

transformer layers包含a self-attention module and a feed-forward network
为SAN和FFN引入一个称为“可分解性decomposability”的重要属性，这表明SAN或FFN中的每个子组件都是独立计算的，而子组件之间没有相互作用，因此它们可能是冗余的。

• decomposable的定义: A computing module $f$ 是 decomposable， 如果他的 sub-components $\{g_1, g_2, \cdots g_H \}$ 可以独立计算:$ f(x) = \delta\big(g_1(x) ,g_2(x), \cdots, g_H(x) \big)$. 通常 $\delta$ 是一个相对$\{ g_h\}$可以忽略不计的简单操作 特别是，如果$\delta$是级联或加法，则子组件之间的反向传播是独立的。$f$中的子组件可以在没有交互的情况下并行计算。我们将检查SAN和FFN是否是可分解的。

decomposability in SAN.SAN可以分解成每个head的输出之和。For the query/key/value/output transformations parameterized by $W^Q / W^K / W^V / W^O$, we divide them as $N_h$ heads: $\{W^Q_h\}^{N_h}, \{W^K_h\}^{N_h}, \{W^V_h\}^{N_h}, \{W^O_h\}^{N_h}$. A single head is calculated as

$$\begin{equation} \small \textrm{Att}_h (X) = \textrm{Softmax}( \frac{1}{\sqrt{d}} X W^Q_h {W^K_h}^T X^T) X W^V_h {W^O_h}^T \end{equation}$$

Then $\textrm{SAN}(X) = \sum_{h=1}^{N_h} \textrm{Att}_h (X)$, indicating SAN is decomposable.
头部之间的注意力由于独立计算而学习冗余的密钥/查询投影。

decomposability in FFN
FFN中的两个权重矩阵, $W^{In}$ and $W^{Out}$.

$$\begin{equation} \label{sec:ffn} \small \textrm{FFN}(X) = \sum_{h=1}^{4D} \textrm{GeLU} (X W^{In}_{\cdot,h} + b^{In}_{h} ) W^{Out}_{h,\cdot} + b^{Out} \end{equation}$$

FFN也作为一种类似于SAN的键值机制运行：可以将FFN的输入视为查询向量，将两个线性层的FFN分别视为键值。可能存在一些可能引入冗余的类似键值对。

expoloration of a pre-trained transformer

Transformer的主要权重矩阵$\{W^Q,W^K,W^V,W^O, W^{In}, W^{Out}\}$，（FFN能以a multi-head fashion来分别计算的，我们将其分组为$\{ W^{In} \}$ and $\{ W^{Out} \}$ into four groups like $\{ W^{In}_h \}^{h=4} $ and $\{ W^{Out}_h \}^{h=4} $ respectively.）。
这样操作后，所有的权重矩阵reshape为$D\times D$，此时得到了12个$D\times D$矩阵（4个来自SAN，8个来自FFN）

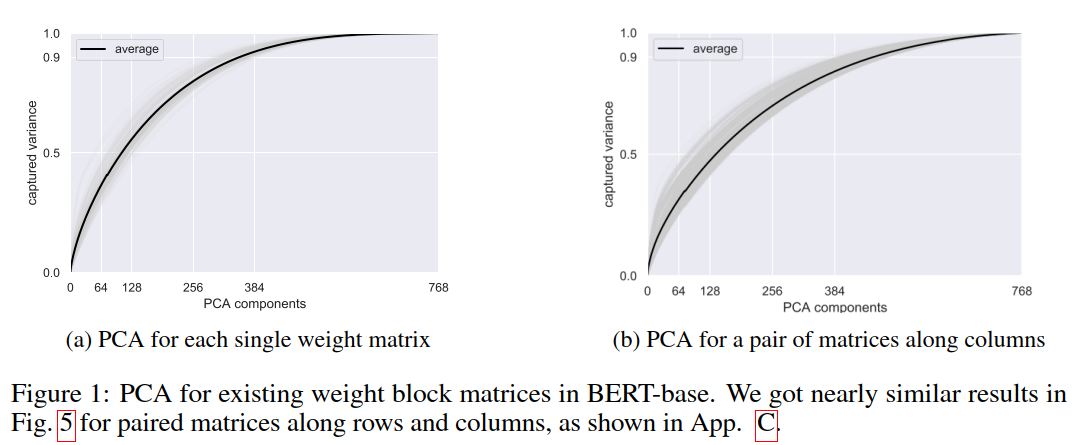
如上可以发现 intra-matrix and inter-matrix redundancy。
图1a看到只需要half dimensions的PCA就可以得到80%的方差， 还通过进行在两个任意配对的权重矩阵之间的级联矩阵上的PCA。见图1b，半维可以捕获近80%的方差，这表明压缩矩阵间冗余的可能性。这种矩阵间冗余可能是双重的：
（1）子FFN是可分解的；
（2）不同层中的计算（例如注意力图）可以是相似的。

exploring parameter compression

我们将不同layer的SAN以及FFN中的权重矩阵堆叠在一起，第$j$-th transfomer的weight matrices为

$$\begin{equation} W^{(j)} = \left[ \{W^Q,W^K,W^V,W^O\} \oplus \{ W^{In}_h \}^{h=4} \oplus \{ W^{Out}_h \}^{h=4} \right]_j \in \mathbb{R}^{12 \times D \times D}. \end{equation}$$

对于L层的transformers而言，其权重矩阵可以堆叠为三阶张量大小为$12L\times D\times D$, The original non-decomposed weights is called Ⅰ: $W^{Ⅰ} = \{W^{(j)}\}_{j=1}^{L} \in \mathbb{R}^{12LD^2}$. Each weight matrix in $W^{Ⅰ}$ is $W_i^{Ⅰ} = W_i \in\mathbb{R}^{D \times D}$.

Ⅱ matrix decomposition. 受intra-matrix redundancy的启发，可以采用矩阵分解将矩阵分解/近似为一些较小的矩阵。一种典型的方法就是SVD，called Ⅱ-$\alpha$, for each $D\times D$ matrix $W_i \in\mathbb{R}^{D \times D}$

$$\begin{equation} W_i \approx W_i^{Ⅱ}= U_i \Sigma_i V_i \in \mathbb{R}^{D\times D} \end{equation}$$

One can also drop the diagonal ${\Sigma_i}$ by decomposing it into two parts that are multiplied to $U_i$ and $V_i$, namely $W_i \approx U_i V_i$, denoted as `Ⅱ-$\beta$’. $U_i \in \mathbb{R}^{D \times d} $ and $V_i \in \mathbb{R}^{d \times D}$ and usually $d< D$. Since the compression ratio is $\frac{D^2}{2Dd}$ with reducing the rank from $ D$ to $d$, 近似矩阵的保留秩随着压缩率线性地减小。

Ⅲ tensor train decomposition. 受inter-matrix redundancy的启发，可以在矩阵之间共享参数。
在SVD中最大的矩阵是$U_i$和$V_i$ 因为$\{ {\Sigma_i} \}$ 相对其他矩阵参数量少。我们可以共享矩阵间的分解结果中的$ \{ U_i \}$和$ \{ V_i \}$,对于每个权重矩阵

$$\begin{equation}\label{eq:tt} W_i \approx W_i ^{Ⅲ} = U V \in \mathbb{R}^{D \times D} \end{equation}$$

Here, $\{ {\Sigma_i} \}$ 不一定是对角线的。 This results in a tensor-train(TT) decomposition.

A tensor-train decomposition is to approximate a high-order tensor with a product of many smaller three-order tensors — except for the first and last ones being matrices. Here, for a three-order tensor $W \in \mathbb{R}^{12L \times D \times D}$, it is approximated by $W \approx U G V$ and shape transpose, where $U \in \mathbb{R}^{D \times r_1}$, $G \in \mathbb{R}^{r_1 \times 12L \times r_2}$, and $V \in \mathbb{R}^{r_2 \times D}$. For a specific slice of $W$, $W_i \approx U G_{\cdot,i,\cdot} V$. $r_1$ and $r_2$ are the `TT ranks’.

还可以考虑更高阶的TT分解（即，张量乘法的较长链），这可能更具参数效率；这通常需要用启发式方法将原始张量重塑为高阶张量。然而，在训练过程中，它更耗时，占用更多的GPU内存，我们将其作为未来的工作。

Ⅳ tucker decomposition. 在上式中，最大的项是 $\{ {\Sigma _i} \} \in \mathbb{R}^{ 12L \times d^2}$，特别是当模型的层数很大时。本文提出了一种固定尺寸的{matrix bank} 使得权重矩阵被视为bank中的矩阵的线性组合，使得参数尺寸相对于层数几乎不变。

$$\begin{equation}\label{eq:tucker} W_i \approx W_i ^{Ⅳ} = U (P _i C ) V \in \mathbb{R}^{D \times D} \end{equation}$$

where $C \in \mathbb{R}^{l \times d^2}$ is a matrix bank with a size of $l$, each matrix is assigned with a weight vector $ P_i \in \mathbb{R}^{1 \times l} $.
ALBERT could be considered as a special case of $Ⅳ$.

comparison between these decomposition

下图表示这些分解方法的的参数规模。

由于$D>d$和$L>l$，我们通常可以得出结论，参数尺度从Ⅰ Ⅱ Ⅲ 减小到Ⅳ。我们可以观察到，在Ⅳ中添加新层的边际参数成本接近$12l$，与其他参数相比可以忽略不计。在推理阶段，不涉及批量大小$b$或序列长度$n$的项在开始推理之前只能以离线方式计算一次，这需要更多的存储空间，但会略有加速-由于这项工作的主要目的是压缩模型，我们在这项工作中忽略了它，但鼓励在速度敏感的场景中这样做。

extremely compressing bert using tensor decomposition

decomposition protocol

Ⅳ 减少空间复杂度从 $\mathcal{O}(12LD^2) $ 到 $\mathcal{O}(l d ^2 + 12L l + 2Dd ) $ where $d<D$ and $l < 12L$.
$l$决定了我们希望在所有模块之间共享Transformer参数的程度，这是一个灵活的因素，可以将普通BERT平滑地转换为layer-shared BERT（或称为“ALBERT”）$d$决定了每个线性变换的表达能力（秩）（最初为$D\times D$）。
估计权重矩阵总是与原始矩阵有些差距。由于多层神经网络架构，低层中权重矩阵的微小分解差异可能导致最终输出的累积差异，我们建议使用知识蒸馏来模拟原始模型的最终输出。

$$\begin{equation} f_{W^{Ⅰ}} (x) \approx f_{W^{Ⅳ} } (x) \end{equation}$$

$f_{W ^ {Ⅰ}}$是原始BERT模型，$f_{W^{Ⅳ}}$是压缩模型。我们认为，预测中的近似（如方程7中的知识提取）比权重中的近似更重要。这种压缩中的损失感知策略可以在量化中找到。

reconstruction protocol

$D \times D$ 参数块的一个切片表示为矩阵乘积，$W_i^{Ⅳ}\approx U(P_i C)V\in\mathbb{R}^{D \times D}$.
对于输入$X \in \mathbb{R}^{b \times n \times D}$，其中b是批大小，n是序列长度，X和D×D参数块之间的线性变换的输出将是$Y = X{W}_{i;;} = XU(P_i C)V$.由于矩阵乘法是满足分配律，不同的乘法分配不会影响最终结果，但它们的计算复杂度可能不同。可以在表3中看到乘法阶的计算复杂性。在实践中，批量大小b将设置得尽可能大，以增加数据吞吐量并使训练更加稳定，我们可以得出结论，IV-3比IV-2更有效。
当$D>2d$, IV-3比IV-1更有效。；在实践中D通常比d大得多并且$D>2d$。总之，在这种情况下，设置IV-3是最有效的。

Experimental Design and Results

settings

decomposition. 对于BERT-base($L=12, D=768$),权重矩阵为$W^Ⅰ \in \mathbb{R}^{144 D^2}$被分解为三种因子矩阵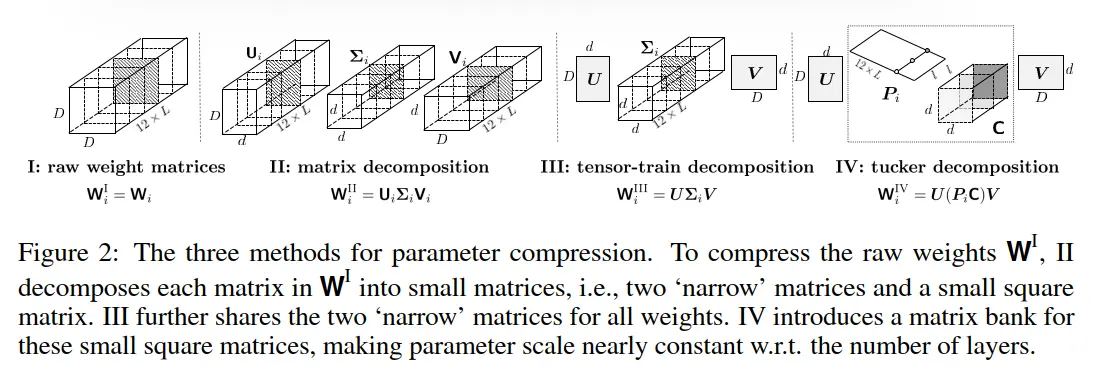

Knowledge distillation. 对于压缩模型，我们使用两阶段知识提取。在普通蒸馏（GD）阶段，
我们采用知识蒸馏（KD）作为压缩模型来模拟通用教师模型（BERT库）的最后一层隐藏状态和最后一层注意力图。在第二阶段，
我们采用任务特定蒸馏（TD）来模拟任务特定BERT模型的logits（例如。fine-tuned on MNLI任务）。在GD中，压缩模型用两个时期进行训练。在TD中，我们还通过使用Glove根据词向量相似性或掩蔽目标词时BERT的预测物流，用相似词随机替换随机词来扩充训练数据，

GLUE evaluation. GLUE的微调和评估遵循Huggingface的设置。根据开发集选择性能最佳的模型，其中我们在[1e-5，2e-5]中选择学习率，在[16，32]中选择批量大小。

1. 结果
   性能：其中一个配置，BERT-III-384，以Transformer层仅1/7的参数超越了BERT-base的性能，并略微增加了吞吐量。另一个模型，BERT-IV-72-384，以更少的参数与原始BERT模型表现相当。
   压缩与效率：BERT-III和BERT-IV模型展示了在保持或略微提高GLUE基准任务性能指标的同时，实现极端压缩的潜力。文档特别强调了像BERT-III-64这样的模型，仅使用Transformer层1/48的参数就达到了BERT-base性能的96.7\%，并在推理速度上实现了2.7倍的加速。

1. 消融研究
   知识蒸馏的必要性：一个消融研究确认了GD和TD阶段在实现压缩模型有效性能中的关键作用。去除TD显著降低了总体性能。
   对FFNs或SANs的分解：尝试分别压缩前馈网络（FFNs）或自注意力网络（SANs），结果显示两者几乎可以匹敌原模型的性能。FFNs显示出略好的可压缩性。

Comparative Analysis

Discussion and Limitations

Conclusion