Paper-Analysis-LQ-LoRA: Low-rank Plus Quantized Matrix Decomposition for Efficient Language Model Finetuning

Title and Authors

LQ-LoRA: Low-rank Plus Quantized Matrix Decomposition for Efficient Language Model Finetuning

Background and Motivation

LLM的庞大规模使得他们通过全面finetuning来适应新数据集的成本很高。memory-efficient LLM adaption方法其中的一个方法使用parameter-efficient finetuning方法，这些方法可以学习到一个基于pretrained model的更小的微调扩展，可以减少微调所需的内存量。这是因为pretrained parameters 会 remain fixed，从而减少了为存储这些参数的梯度和优化器状态分配内存的需求，从而要优化的新参数的数量只是固定参数的一小部分。

2022年 Hu 等人提出了一个low-rank adaption,预训练模型的权重矩阵被重新参数化$W+L_1L_2$且只有L1和L2被微调.近期也有一些方法来改进LoRA,来使用一个quantized pretrained model $q(W)+L_1L_2$,这里$q(\cdot)$是某种quantization function.

LOW-RANK ADAPTION OF LLM

low-rank adaption是2022年提出的一种简单有效的LLM内存开销减少办法。给定一个pretrained linear layer的权重矩阵$W\in \mathbb{R}^{d\times r}$，LoRA初始化两个$L_1\in\mathbb{R}^{d\times r}, L_2\in\mathbb{R}^{r\times k}$，其中$r<\min(d,k)$，$L_1$初始化为Gaussian noise以及$L_2$被初始化为0.LoRA将linear layer重新参数化为$X(W+L_1L_2)$，$X$是之前层的激活值，在language model adaption中只需要微调$L_1L_2$.
LoRA比full fientuning更有效，因为不需要为gradients和相关的优化器状态（例如Adam的动量和variance statistics）分配GPU内存。更重要的是用于内存高效微调的其他策略也可以在预训练模型上学习少量的参数以及prompt tuning。因此LoRA因适应LLM而广受欢迎。

weight quantization of LLMs

权重量化（Weight Quantization）：权重量化是一种将神经网络中的权重参数从浮点数值转换为较低精度的整数值的技术。这有助于减小模型的存储需求和加速推断过程。
Round-to-Nearest（RTN）量化：这是一种标准的量化方法，它将权重量化为一个整数值，其计算方式为将权重除以一个缩放因子，然后将结果四舍五入到最接近的整数。这个缩放因子根据权重的范围和所需的位数进行计算。这个方法在8-bits上被证明进行量化LLM的预训练权重是有效的。但是对于(sub)4-bit量化，使用RTN非常困难。因此研究人员使用一种数据感知策略，通过calibration samples来获得更好的权重量化结果。
NormalFloat（NF）量化：NF量化方案利用了训练模型的权重分布近似为高斯分布的事实。NF量化将权重分成一系列概率值和相应的量化点，然后将权重映射到最接近的量化点。

QLoRA是一种基于NF量化的方法，它在预训练的LLM上执行4位NF量化，并学习低秩更新。它已经在多个基准测试中表现出竞争力。

Main Contributions

在LoRA中, L2被初始化为0来确保模型输出与finetuning初期保持一致 $X(W+L_1L_2)=XW$.然而,如果预训练矩阵被量化到会发生大量的量化误差的程度(sub-4-bit regimes),则零初始化可能不是最优的,因为$q(W)+L_1L_2\neq W$.
因此本文考虑LoRA仅对量化模型进行低秩更新的前提下,推导出一个考虑量化误差的初始化方案.
本文参考robust PCA中的迭代方法,来分解W, $W\approx Q+L_1L_2$.这里$Q$是保持fixed的quantized component而$L_1L_2$(获取$W$的high-variance subspaces)参与finetuning.本文不将相同的量化配置应用于所有层,而是使用整数线性规划来找到允许分配不同配置的混合量化策略(bits, block size等),最后探索了该算法的数据感知版本.
应用LQ-LoRA来改编RoVERTa和LLaMA-2模型,发现它比QLoRA和GPTQ-LoRA更好,同时用户能自由设置目标内存.

Theoretical Framework/Algorithm

我们的方法依赖于一个简单的因子分解方案，该方案将每个预训练的矩阵分解为一个低秩矩阵加一个量化矩阵（§3.1），其中在微调过程中只调整低秩分量。在§3.2中，我们通过整数线性规划探索了一种混合量化策略，以允许在给定目标平均比特率的情况下跨层动态量化。我们进一步考虑LQ-LoRA的数据感知版本，通过使用经验Fisher信息矩阵在矩阵分解过程中对重建目标进行加权（§3.3）。

low-rank plus quantized matrix decomposition

LoRA确保了模型输出与微调开始时的重新参数化之前完全相同，但在使用W的量化版本时可能会出现问题。当量化到low bits，有$| W-Quantize(W)| _F >> 0$.在决定适应哪些子空间时，这种初始化不考虑W的结构。我们从矩阵分解的角度来处理这个问题，其中我们感兴趣的是将原始矩阵分解为易于量化的分量和捕获高方差方向的低秩分量，

$$\begin{equation} \begin{aligned} &argmin_{\mathbf{Q}, \mathbf{L}_1, \mathbf{L}_2} \, \Vert W - (Q + L_1 L_2) \Vert_F, && \text{where} \,\, Q \in \mathbb{Q}_b^{d \times k}, L_1 \in \mathbb{R}^{d \times r}, L_2 \in \mathbb{R}^{r \times k}. \label{eq:lpq} \end{aligned} \end{equation}$$

这里，$\mathbb{Q}_b^{d \times k}\subset \mathbb{R}^{d \times k}$是可无损NF量化为b比特的矩阵集。

在量化过程中，选择哪些子空间（即哪些权重方向或分量）进行保留可以帮助模型在低比特位下仍然保持较好的性能。这种选择通常需要考虑权重的结构和重要性，以便在量化后最大程度地保留模型的表达能力。

本文使用alternating 来优化$L_1L_2$ 和 $Q$

$$\begin{equation} \begin{aligned} L_1^{(t)}, L_2^{(t)} &\gets \operatorname{SVD}(W - Q^{(t-1)}, r), && \hspace{0.5cm} {\color{gray} = argmin_{rank(L) \le r} \, \Vert W - (Q^{(t-1)} + L) \Vert_{F},} \\ Q^{(t)} &\gets \operatorname{Quantize}(W - L_1^{(t)} L_2^{(t)}), && \hspace{0.5cm} {\color{gray} \approx argmin_{Q \in \mathbb{Q}^{d \times k}_b} \, \Vert W - (Q + L_1^{(t)}L_2^{(t)}) \Vert_F,} \end{aligned} \label{eq:lpq-steps} \end{equation}$$

上述算法是启发式的。因此，我们采用了一个简单的停止准则，其中我们跟踪误差$\Vert W - (Q^{(t)} + L_1^{(t)} L_2^{(t)}) \Vert_F$，并在误差增加时终止算法。算法如下所示

下图表示不同分解方式的误差，左边图中，展示了分解误差随着迭代变化情况，关注的是LLaMA-2-7B的一些layers。中间这个图表示的是对于3-bit的NF量化的量化误差，右边表示的是本文提出的LQ分解的量化误差。对于这两种方法，我们发现value和output projection matrices在更深的层变得更难量化，而key矩阵和query矩阵变得更容易；然而，我们的LQ分解能够改进所有层的vanilla量化。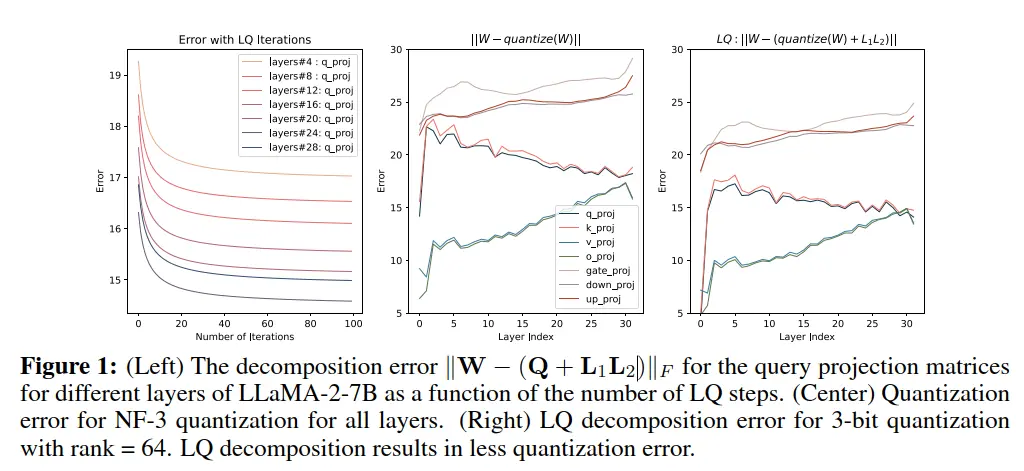

mixed-configuration quantization via an integer linear program

LQ-LoRA使用NormalFloat（NF）量化方案来量化每个时间步长的残差Q。NF量化有几个影响整体压缩率的参数，例如分位数仓的数量、块的数量和用于双重量化的比特the number of quantile bins, number of blocks, and bits for double quantization。
在本文中，我们使用稍微不同的变体，该变体通过以下方式量化矩阵A：

$$\begin{equation} \begin{aligned} \widehat{A}, s = \operatorname{Quantize-NF}\left(A, b_0, B_0 \right), \,\,\,\,\,\,\,\, & \widehat{s}, v = \operatorname{Quantize-INT}\left(s, b_1, B_1 \right), && \widehat{v} = \operatorname{cast}\left( v, b_2 \right). \end{aligned} \end{equation}$$

此量化方案要求存储 $\widehat{A}, \widehat{s}, \widehat{v}$ to represent $A$. 因此，我们可以量化 the storage cost (number of bits) for storing $A$ given a configuration $c = (b_0, b_1, b_2, B_0, B_1)$ as

$$\begin{equation} \operatorname{storage}(A, c) = \operatorname{sizeof}(A) \cdot \left( b_0 + \frac{b_1}{B_0} + \frac{b_2}{B_0 \cdot B_1} \right). \label{eq:storage} \end{equation}$$

先前关于量化LLM的工作通常集中于将相同的量化策略应用于每个矩阵，这不能适应用户变化的资源约束，而且考虑到一些矩阵可能比其他矩阵更难量化，这可能是次优的。我们探索了一种基于整数线性规划的混合精度量化策略（Yao et al.，2021；唐等人，2022；Kundu et al.，2022），该策略允许在给定用户定义的目标目标比特率的情况下为每个矩阵分配不同的配置。

这是一个关于动态权重量化配置的方法，该方法旨在根据不同的资源限制和权重矩阵的性质为每个权重矩阵选择合适的量化策略。

• 首先，它介绍了配置参数，这些参数用于表示不同的量化策略。这些参数包括位宽（$b_0$、$b_1$、$b_2$）、块大小（$B_0$、$B_1$）等，用户可以定义一组可能的配置，以满足其需求。

• 然后，文中提到了一个搜索空间 $\mathcal{C}$，它包含了所有可能的配置组合。在这个示例中，搜索空间的具体设置如表格所示，包括不同的位宽和块大小选项。

• 

接下来，文中提到了一个目标和约束问题。目标是找到一种分配方式，使得在进行低秩加量化分解之前和之后的权重矩阵之间的Frobenius范数差异最小，同时要求满足用户定义的内存预算。这是一个整数线性规划问题，其中涉及到了两个主要方面：

目标函数：最小化矩阵的重构误差，其中 $\operatorname{error}(W^{(i)}, c^{})$ 表示使用配置 $c$ 进行量化后的矩阵 $W^{(i)}$ 与低秩加量化分解后的矩阵之间的Frobenius范数差异。

约束条件：确保总存储空间不超过用户定义的内存预算，以及每个权重矩阵都被分配到一个配置。

$$\begin{equation*} \begin{aligned} &\min_{X \in \{0, 1\}^{N \times |\mathcal{C}|}} && \sum_{i \in [N]} \sum_{c \in \mathcal{C}} \operatorname{error}(A^{(i)}, c) \cdot \mathbf{X}[i, c], \\ & \text {subject to} && \sum_{i \in [N]} \sum_{c \in \mathcal{C}} \operatorname{storage}(A^{(i)}, c) \cdot \mathbf{X}[i, c] \leq \text{budget}, \\ & &&\sum_{c \in \mathcal{C}} \mathbf{X}[i, c] = 1, \quad \forall i \in [N]. \end{aligned} \label{eq:ilp} \end{equation*}$$

为了解决这个整数线性规划问题，研究人员进行了一次预计算，计算了各个矩阵和配置的重构误差。然后，使用专业的求解器来找到（近似）最佳配置分配。这个过程可以在预处理阶段完成，而且只需要一次，预处理过程可以并行化，所以速度较快。

最后，一旦找到了最优配置，就可以将这些配置应用于每个权重矩阵，进行低秩加量化分解，以获得最终的量化矩阵。这个方法的优势在于它可以根据不同的权重矩阵和资源限制，自动选择最佳的量化配置，从而提高了量化后模型的性能。

实现方法：现有的权重量化实现通常依赖于特定的CUDA扩展，这使得难以将其扩展到混合量化策略上。与此不同，作者选择了基于PyTorch的实现，以获得更大的灵活性和易用性。
他们使用了PyTorch的特殊功能，即torch_dispatch，来模拟PyTorch张量，并通过操作重载实现了即时的反量化功能。这意味着当需要对量化后的张量执行操作时，系统会自动进行反量化，以便在计算中使用原始的浮点数值。
此外，他们还充分利用了PyTorch的编译器，将位解压、反量化和其他线性代数操作进行了编译，以提高计算效率。值得注意的是，对于批量大小大于1的情况，这种基于PyTorch的实现（经过编译）在性能上表现得与一些自定义的CUDA实现相当。

data-aware matrix decomposition via fisher-weighted svd

前文中的分解目标是数据不可知的，因为它将$W$中的每个entry在分解期间的重构中同等重要，最近的工作证明了使用校准数据量化LLM的重要性。使用Fisher信息矩阵的对角近似来加权重建目标，来考虑该方法的数据感知版本。W的经验Fisher信息矩阵的（对角线）由下式给出，其中每个entry是D个样本的倒数的平方平均值
$
F_{ij} = \frac{1}{D} \sum_{d=1}^{D} \left( \frac{\partial}{\partial W_{ij}} \log p_{\text{LM}}\left(x^{(d)}\right)\right)^2.
$
该指标测量模型的输出表示对每个参数的扰动的敏感度，并且之间已经被用于改进预训练language model的低秩压缩，因此使用F来加权分解目标

$$\begin{equation} \begin{aligned} \left\Vert {\sqrt{F}\, \odot } \left(W - \left(Q + L_1 L_2\right) \right) \right\Vert_F^2, \end{aligned} \label{eq:weighted-error} \end{equation}$$

where $\odot$ is the Hadamard product.应用到前文的LQ分解，定义$E:=W-Q$,有

$$\begin{equation} \begin{aligned} \mathbf{L}_1, \mathbf{L}_2 = argmin_{\mathbf{L}_1, \mathbf{L}_2} \; \left\Vert \sqrt{\mathbf{F}} \odot \left( E - \mathbf{L}_1 \mathbf{L}_2\right)\right\Vert_F^2 . \end{aligned} \end{equation}$$

这是个NP难问题，但如果我们假设权重矩阵F的行或列具有相同的值，则我们具有以下恒等式，

$$\begin{equation} \begin{aligned} \mathbf{L}_1, \mathbf{L}_2 = argmin_{\mathbf{L}_1, \mathbf{L}_2} \; \left\| \sqrt{\mathbf{F}} \odot \left( E - \mathbf{L}_1 \mathbf{L}_2\right)\right\|_F^2 \\ = argmin_{\mathbf{L}_1, \mathbf{L}_2} \; \left\| \mathbf{D}_{\text{row}} \left( E - \mathbf{L}_1 \mathbf{L}_2\right)\mathbf{D}_{\text{col}}\right\|_F^2, \end{aligned} \end{equation}$$

where $\mathbf{D}_{\text{row}}$ is a diagonal matrix consists of row-means of $\sqrt{\mathbf{F}}$, and $\mathbf{D}_{\text{col}}$ is a diagonal matrix consisting of the column-means of $\sqrt{\mathbf{F}}$, i.e.,

$$\begin{equation} \begin{aligned} \mathbf{D}_{\text{row}} {=} \operatorname{diag}\left(\left[ \operatorname{avg}(\sqrt{\mathbf{F}_{1, \cdot}}), \dots, \operatorname{avg}(\sqrt{\mathbf{F}_{d, \cdot}}) \right]\right), \mathbf{D}_{\text{col}} {=} \operatorname{diag}\left(\left[ \operatorname{avg}(\sqrt{\mathbf{F}_{\cdot, 1}}), \dots, \operatorname{avg}(\sqrt{\mathbf{F}_{\cdot, k}}) \right]\right). \end{aligned} \end{equation}$$

In this case the above problem can be solved exactly by standard SVD,

$$\begin{equation} \begin{aligned} \mathbf{U}, \Sigma, \mathbf{V}^\top \gets \operatorname{SVD}(\mathbf{D}_{\text{row}} A \mathbf{D}_{\text{col}}), \,\,\,\,\, & \mathbf{L}_1 \gets \mathbf{D}_{\text{row}}^{-1} \mathbf{U} \sqrt{\Sigma}, && \,\,\,\,\, \mathbf{L}_2 \gets \sqrt{\Sigma} \mathbf{V}^\top \mathbf{D}_{\text{col}}^{-1}. \end{aligned} \label{eq:custom-weighted-svd} \end{equation}$$

虽然齐次行/列假设显然不适用于F，但我们发现这种方法在实践中效果良好。9我们注意到，这种近似是Hsu等人的简单扩展。（2022）他们在加权SVD中使用Drow，但不使用Dcol（我们发现同时使用行和列平均值的效果略好）。

LQ-LoRA的这种数据感知版本需要能够通过预训练的LM进行反向传播，以获得Fisher矩阵{F（i）}i∈[N]，在某种意义上，这违背了memory-efficient adaptation methods所针对的设置，其中完全微调被认为是不可能的。这是一个有效的观点，因此我们在实证研究中研究了LQ-LoRA的两个版本。然而，我们注意到，我们基于一些通用文本数据计算{F（i）}i∈[N]，以获得LQ-LoRA初始化{Q（i），L1（i）、L2（i）}i∈[N]，并对不同的下游任务使用相同的初始化。这使得数据感知方法变得实用，因为Fisher计算和矩阵分解只需要执行一次（如在非数据感知版本中）。

Experimental Design and Results

我们在三个settings下进行实验：

1. continual language modeling on C4 training data
2. instruction tuning on the OpenAssistant dataset
3. finetuning on GLUE
   对于1和2，我们使用LLaMA-2模型，而对于3，我们使用RoBERTa-Large。设置密切遵循Dettmers等人的设置。（2023a）。LQ-LoRA的Fisher加权版本使用来自C4训练集的随机采样序列，其中对于RoBERTa Large，我们使用masked language modeling objective（也在C4上）来获得Fisher矩阵。

baselines

我们的主要基线包括QLoRA和GPTQ-LoRA。这两种方法在学习对量化模型的低秩更新以进行自适应之前，对预训练的模型执行PTQ；QLoRA使用NF量化，而GPTQ-LoRA使用近似二阶信息来求解$argmin_{\hat{ W} \in \mathbb{Q}_{b}^{d \times k}}\Vert X W - X\ \hat{ W}\Vert_F$。在我们的主要实验中使用秩=64，并在我们的分析部分中讨论消融该秩。

evaluation

为了评估在C4上的模型，我们使用了三个指标

• perplexity on C4 validation
• perplexity on WikiText-2
• 5-shot MMLU accuracy
  对WikiText-2的评估是为了确保语言模型不会通过LoRA微调过度拟合到C4数据集。

对于instruction tuning，我们使用Vicuna-style automatic evaluation。这包括要求GPT-4在对于超过80个精心策划的问题其输出和GPT-3.5的输出之间进行配对比较（可能出现平局）。根据Dettmers等人的建议设置，我们选择了这种评估方案，而不是10分评分系统。（2023a）。

对于GLUE基准，我们显示了所有任务的平均指标。

training details

除非另有规定，我们使用64 rank，没有LoRA dropout，默认学习率为2×10−5，只有少数例外。

对于continual language modeling，我们 train on one partition of the C4 data for half an epoch，使用1024的序列长度进行训练和评估。

为了估计Fisher，我们使用序列长度为1024的C4的10000个样本。

对于GLUE任务，我们使用类似的设置，但在C4上使用屏蔽语言建模目标。

对于instruction tuning，我们使用Dettmers等人建议的超参数。（2023a）（除LoRA dropout）。

对于GLUE微调，我们遵循Hu等人推荐的学习率和时期数量。（2022）QLoRA基线。然而，由于MNLI和QQP的大小，我们只微调了5个时期的模型。

Language Modeling和指令调优实验：

• 方法：在实验中，研究人员使用了LLaMA-2模型，并对不同模型大小和指标进行了语言建模和指令调优。他们比较了LQ-LoRA、QLoRA和GPTQ-LoRA在相似位数预算下的性能。
• 结果：实验结果表明，LQ-LoRA在大多数情况下几乎总是优于QLoRA和GPTQ-LoRA。例如，3.5位（Fisher）的LQ-LoRA通常与需要4.127位/参数的NF-4位QLoRA性能相当；同样，2.75位的LQ-LoRA与需要3.127位/参数的NF-3位QLoRA竞争力相当。这突显了混合量化方案的实用性，因为没有ILP，这些混合策略甚至不会被发现。不过，需要注意的是，当接近2.5位时，性能开始显著下降。在较小的7B规模上，Fisher加权的LQ-LoRA在所有目标位宽下都优于未加权的版本，但在70B规模上，这种差异缩小了。

• LQ-LoRA用于模型压缩：

• 方法：在这个实验中，研究人员使用LQ-LoRA来进行模型压缩，针对C4和WikiText数据集进行了实验，并测量了特定子集数据上的性能，通过困惑度来评估。

• 结果：研究发现，使用2.75位的LQ-LoRA进行模型压缩时，考虑到LoRA组件后，7B和70B模型的平均位数分别为2.95位和2.85位。这通常优于其他低于4位的PTQ方法，这些方法也使用了校准数据来量化预训练模型。这表明LQ-LoRA是一种有效的模型压缩技术。

零/少次迁移能力评估：

• 方法：研究人员使用Eleuther AI语言模型评估工具在多个基准任务上评估了LQ-LoRA的零/少次迁移能力。他们评估了模型在不同任务上的性能。
• 结果：实验发现，在某些基准任务上存在一定程度的性能下降，这表明困惑度的下降并不总是与零/少次迁移性能的变化成比例关系。这强调了在不同任务上评估模型性能的重要性。

存储需求分析：

• 方法：研究人员分析了不同位数下模型的存储需求，将存储分为不同部分，包括非量化部分、量化部分和LoRA参数。
• 结果：实验结果显示，在低于3位的量化下，模型所需的存储显著减少，这使得可以在单个GPU上运行70B模型。对低于3位的模型进行微调需要更多的内存，但他们成功地在单个80GB GPU上以批量大小为2和序列长度为2048的情况下运行了完整的前向/后向传播。
  总的来说，这些实验支持了LQ-LoRA作为一种有效的模型量化和压缩技术的潜力，特别是在资源受限的环境中，同时也提供了关于性能、扩展性和存储需求的有用信息。
  <!— ## results
  图2显示了LLaMA-2上不同模型大小和度量的language modeling and instruction tuning结果。
  表明LQ-LoRA混合量化策略在不同模型尺寸和性能指标下的优越性，尤其在相对低的位宽条件下。这种策略的性能提升归功于混合量化，而混合策略的发现得益于整数线性规划方法的应用。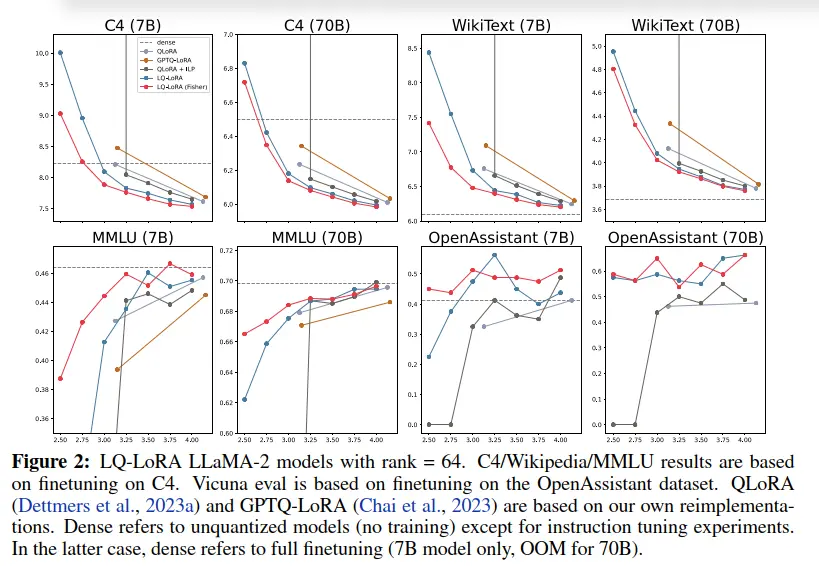
  

LQ-LoRA for model compression —>

Comparative Analysis

Discussion and Limitations

1. 迭代算法和优化方法：作者提到他们使用的迭代算法在实验中表现良好，但仍然是一种经验性的启发式方法。他们表示，未来的研究可以探索更具理论基础的优化算法，以提高LQ-LoRA的性能。此外，他们还建议在其他量化方法的基础上应用LQ分解，可能会带来更好的效果。

2. 混合精度和混合秩分解：研究人员提到可以将ILP-based混合精度方法扩展到混合精度量化和混合秩分解，以允许为每个矩阵分配不同的秩。然而，他们指出这可能不是最优的，因为ILP只最小化了分解误差，而没有考虑最终的下游性能。他们提到，可以通过在ILP中将LoRA参数视为更不昂贵（因为可微调的参数对于下游性能贡献更多），以解决这个问题。

3. 负面结果和局限性：研究人员还讨论了一些负面结果和LQ-LoRA的局限性。他们发现，周期性地重新因子化矩阵（例如，在每个$K$个梯度步骤之后）并没有改善性能。此外，他们尝试了一种混合方法，其中一半可调整的低秩组件来自LQ-LoRA，另一半来自标准的LoRA初始化，但并没有发现这能够改善结果。最后，他们指出，他们的方法在很大程度上依赖于适应通过低秩更新来实现，因此不适用于其他参数高效的微调方法。这些局限性和负面结果提供了对LQ-LoRA的一些限制和改进方向的思考。

   Conclusion