Paper Analysis: ASVD: Activation-aware Singular Value Decomposition for Compressing Large Language Models

ASVD: Activation-aware Singular Value Decomposition for Compressing Large Language Models

Background and Motivation

有大量的方法用来减少LLM的内存消耗。这些方法可以归类于两种

• neural network compression
  • weight quantization
  • network pruning
  • knowledge distillation
• system optimizations
  • memory management with cache mechanisms

与这些方法不同的是，低秩分解的范式(paradigm)探索较少。该技术涉及使用较低秩的矩阵来逼近神经网络中的权重矩阵，它是一种相对未充分利用的LLM压缩方法。此外，低秩分解通过进一步压缩量化的或剪枝的模型来补充现有的 LLM 压缩技术，从而提高整体效率。

从网络压缩的角度来看，传统的低秩分解方法通常遵循一个简单的过程：首先训练原始模型，然后对分解模型进行微调。但这种方法需要整个训练数据集和大量的计算能力才能进行端到端的反向传播。但在LLMs上不现实。1. LLM的训练数据并不总是容易获得。2. 这些模型的训练过程在时间和计算方面都非常昂贵。基于这些限制，“training-free”压缩成为一种更可行的方法。包括 LLM post-training quantization and LLM post-training pruning, 这些方法都不需要再训练。

• 后训练量化（Post-Training Quantization）：这种方法涉及在模型训练完成后将权重和激活从更高精度（例如32位浮点数）转换为更低精度（例如8位或16位）。这样做的关键好处是显著减少了模型的存储需求和提高了推理速度，而对模型性能的影响通常很小。对于LLMs来说，这是一种有效的压缩手段，因为它不需要再次访问庞大的训练数据集或进行昂贵的训练过程。
• 后训练剪枝（Post-Training Pruning）：这种方法在模型训练完成后进行，它通过识别并移除那些对最终输出影响不大或冗余的权重来减小模型的大小。后训练剪枝的挑战在于找到一个平衡点，即在不显著影响模型性能的情况下尽可能多地移除权重。这种方法同样适用于LLMs，因为它不需要重新训练模型。
• 参数冻结（Parameter Freezing）：在这种方法中，选定模型的某些部分（如特定层或参数）在推理过程中保持不变。这意味着这些部分不需要在推理时进行计算，从而减少了计算成本。这种方法通常适用于那些对输出贡献较小的部分。
• 子网络选择（Subnetwork Selection）：这种方法涉及从原始模型中识别并使用一个更小的高效子网络。这个子网络可以在没有任何额外训练的情况下执行特定任务，从而减少了计算需求。
• 权重共享（Weight Sharing）：在权重共享中，模型的不同部分共享相同的权重集，而不是每个部分都有独立的权重集。这可以显著减少模型的总参数数量。
• 动态稀疏性（Dynamic Sparsity）：这种方法涉及在推理时动态地选择和使用模型中的一部分参数，而不是在每次推理时都使用所有参数。这可以减少计算负担，尤其是在模型需要快速响应的场景中。
• 二值化或三值化网络（Binarization or Ternarization）：这些技术将权重和激活限制为非常小的离散集，如{-1, 0, 1}，从而简化了计算过程。
• 使用激活稀疏性（Leveraging Activation Sparsity）：在某些情况下，神经网络的激活可以非常稀疏。通过利用这一点，可以减少推理过程中的计算负担。
• 结构化剪枝（Structured Pruning）：与传统剪枝相比，结构化剪枝不仅移除单个权重，而是移除整个神经元或卷积核，这可以在不需要重新训练的情况下更有效地减少模型的大小。

为了实现 low-rank post-training decomposition in LLMs, 本文分析了现有的LLM分解方法。发现直接应用现有的低秩分解技术对于LLMs是无效的，分析这些失败的原因后，发现一个关键挑战， managing outliers in the activations, 这些异常值加剧了分解误差。

Main Contributions

• 引入activation-aware singular value decomposition. ASVD将the distribution of activations 合并到分解过程中。它通过根据在输入和输出的channel中观察到的distribution patterns，逐列缩放权重矩阵中的值来实现。事实证明这种调整对于具有异常activations的channels特别有益，允许ASVD将重点放在这些specific weights上。这种针对性的调整有助于更准确地重建weight matrix，因此最小化预测误差以及提升分解过程的效率。

• 进一步深入研究了不同LLM层对分解的不同敏感性。发现multi-head attention layers会比multi-layer perceptron layer更加适应分解。这种对于分解的灵敏度并非在所有层都是一致的，因此本文开发一种方法为每层分配最优的rank。且这个方法很高效，只需要有限的sample set来评估。

• 我们通过吸收分解后的奇异值来优化推理，从而实现计算高效的矩阵运算。我们的方法将奇异值均匀地分布到其他 U 和 V 矩阵中，通过减少量化误差来有利于权重量化
• 应用ASVD到LLaMA和LLaMA-2上，实验表明，ASVD可以有效地将网络权重压缩约10%-20%，而在MMLU等基准测试中，精度仅略有1%的损失。
• 这种压缩是通过免训练的方式实现的，例如 LLaMA-7b 的分解过程，在 Nvidia A6000 GPU 上仅需要 4 个小时。重要的是，我们对 ASVD 与 4/6/8 位量化的兼容性进行了初步验证。 ASVD 作为 LLM 压缩的正交范例出现，无缝集成为与现有 LLM 量化方法一致的即插即用技术。

  Theoretical Framework/Algorithm

low-rank decomposition

现有的针对neural network的低秩分解方法可以分成两类

• fixed low rank
  • 通常使用SVD或者张量分解来分解预训练网络的权重矩阵，然后对分解网络进行微调
  • 它们还涉及约束权重矩阵以在训练期间保持固定的低秩
  • 或将层构建为具有不同rank的层的线性组合
  • 显着局限性是引入了矩阵分解秩作为需要微调的附加超参数

• variable low rank
  • 通过自动确定和调整低秩结构
  • 使用启发式搜索来预先确定分解的rank或者通过一个惩罚评估的矩阵的rank的损失函数来学习低秩权重
  • 消除了选择LLM超参数的需要,并突出了低秩分解作为模型压缩有效工具的潜力,为更高效、可扩展的大语言模型 (LLM) 铺平了道路

difference with TensorGPT

在通过分解进行LLM压缩的方法中，最相关的工作的是并发的TensorGPT，其中embedding layer of LLMs使用tensor-train decomposition进行压缩来以低秩的张量格式来存储large embeddings，并伴随着fewer parameters。区别在与

• TensorGPT只关注于 token embedding matrix, ASVD关注于压缩LLMs的所有权重
• TensorGPT使用固定的rank，而本文使用rank-adaptive.

原始的SVD

在LLM中，最为耗时的是multi-head attention and feed-forward layers中的linear weight matrices。
SVD对于weight matrix的压缩过程可以分为三步：

1. decomposition：将权重矩阵W分解SVD
2. truncation: 保留top的k个奇异值以及对应的right and left singular vectors，这称为$U_k\in \mathbb{R}^{m\times k}, \Sigma_k \in \mathbb{R}^{k\times k}, V^T_k\in \mathbb{R}^{k\times n}$. $k$的选择对于平衡compression ratio和压缩模型性能非常重要。
3. Reconstruction：$W_k=U_k \Sigma_k V_k^T$

在 SVD 上下文中影响模型性能的主要因素是截断误差。这种误差是由于截断的SVD的近似而产生的，这可以通过计算原始权重矩阵W和近似矩阵Wk之间的差值来测量$L_t=| W-W_k|_F=\sum^{min(m,n)}_{i=k+1}\delta^2_i$，这里$\delta_i$是被排除在$\Sigma_k$的奇异值。

使用SVD进行压缩LLMs的挑战

需要在训练，这些方法的主要局限性在于它们依赖于训练数据和大量优化来重新调整分解的模型，这与我们以免训练方式压缩 LLM 的目标形成鲜明对比。这种post-training decomposition of LLMs的主要困难在于

• challenge 1 :sensitivity of weight variation
  近期的论文都强调了考虑activations在压缩LLM的权重中的重要性，不仅考虑权重矩阵的截断误差，还考虑了activations。主要是因为activations中的outliers的重要性，因此对于effective LLM decompsition，目标优化变为

  $$\begin{equation} W^*_k= argmin_{W_k}L(W_k):=\|W_kX-WX\| \end{equation}$$

  这里$X$表示input activations,从小型calibration set中缓存的。这个集合来源于预训练数据集来避免对于特定任务的过拟合。
  相比于完成分解，本文更加关注于确保分解后的LLM的输出与原始LLM的输出非常相似（相比分解效率，更加注重分解的准确性？）。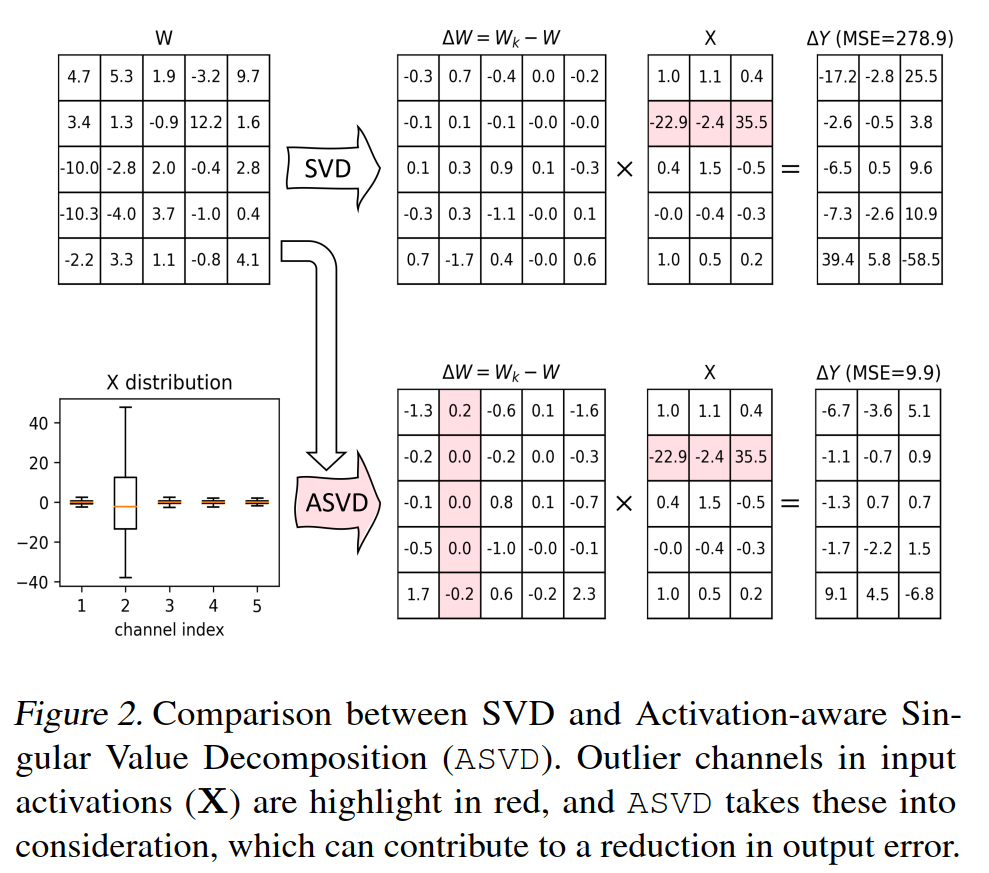
  
  定义activations的variation为

  $$\Delta Y=(W_k-W)X$$

  上图是这个方差的可视化结果。可以发现即使$\Delta$相对较小，但是对应的activations中的variance会很大，这就是为什么直接的SVD分解的效率很低的主要原因。
  尽管activation variance是从input activation(not weight variations)中得出，但是会导致整个模型发生巨大的变化从而破坏分解的有效性。

• challenge 2 singular values variations among layers
  矩阵中奇异值的分布表明了它的稀疏性，进而表明了它对某些类型信息的敏感性。在不同层之间奇异值有很大的差别。在一些层中，大的奇异值会比较集中，这表示他对weight variation相对不敏感，这些层往往很容易压缩。相对的，LLM 中的其他层显示较小奇异值的更均匀分布。这说明不同的层需要一种定制的方法来分解和维护LLM。

为了解决以上的两个挑战，本文提出了两种策略。

activation-aware singualr value decomposition

这个方法在考虑权重矩阵的同时还考虑input activation channels.分为以下三步。

1. scaling the weight matrix.
   使用对角线矩阵$S$来缩放权重矩阵$W$.$S$矩阵用来表示权重的input channels的重要性，本质上是用来调整$W$来更好地使用输入$X$的activation patterns。这个scaled weight matrix $WS$为 $$W=WSS^{-1}=(WS)S^{-1}$$ 因为它修改了权重矩阵以反映不同输入通道的不同意义，为更有效和更有针对性的分解过程奠定基础。$\color{red}{估计是为了突出channel中的outlier， 见上图的红色}$
2. applying svd to the scaled matrix:
   对$WS$应用截断SVD，得到 $$WS\approx U'_k\Sigma'_kV'^T_k$$ 只保留最重要的前k个奇异值的信息。
3. reconstructing the approximated weight matrix $$W\approx U'_k\Sigma'_k(V'^T_kS^{-1})\approx U'_k\Sigma'_kV''^T_k$$ 我们的 ASVD 专注于channel-wise activation outliers，努力通过适当调整相应的权重来减轻这些异常值。通过这种方式，可以减轻活化变化，如图2所示。请注意，S 的对角线性质简化了其反演过程，
   使 $S^{−1}$ 具有计算效率。随后的挑战是设计一种准确确定 S 的方法或标准，使其有效地与 LLM 中观察到的激活模式保持一致，确保缩放过程以最佳方式解决异常激活问题.
4. scaling matrix S exploration
   缩放矩阵 $S$ 中的每个对角线元素，特别是 $S_{ii}$，对于将输入激活调制为 $（WS）X$ 至关重要。$S_{ii}$ 的每个条目都专门缩放第 i 个输入通道的影响。这种缩放有助于调整每个激活通道在分解过程中如何影响权重矩阵。

• Absolute Mean Value of Input Activation: 该方法通过计算第 i 通道中激活的绝对平均值来计算 $$S_{ii}=(\frac{1}{n}\sum_{j=1}^n|X_{ij}|)^\alpha$$ 其中 n 是第 i 个通道的激活总数，超参数α提供了调整缩放中包含的激活灵敏度水平的灵活性。该方法侧重于每个通道中激活的平均幅度，捕获激活信号的一般强度，而不管其正向或负向性质如何。
• Absolute maximum value of input activation: 与基于均值的方法不同，该方法将每个通道内的peak activation归零。在这种方法下，$S_{ii}$ 由在第 i 个通道的激活中观察到的最高绝对值决定。 $$S_{ii}=(\max_j(|X_{ij}|))^\alpha$$ 这种方法强调每个通道中最显着或最高峰的激活，将其作为通道整体影响和重要性的关键指标。通过关注峰值，这种方法强调了具有最明显激活响应的通道，

sensitivity-based truncation rank searching

为了解决第二个挑战，即不同层LLM之间奇异值的变化，我们引入了基于灵敏度的截断秩搜索（STRS）方法。这一挑战源于这样一个事实，即LLM中的不同层对信息压缩表现出不同程度的敏感性，这反映在其奇异值的分布中。STRS旨在分析和利用这种特定于图层的灵敏度，特别是关于奇异值的截断如何影响预测准确性。

我们首先收集一个小而有代表性的校准数据集。该数据集有助于评估图层对不同截断等级的响应能力。对于校准集，我们从维基文本中选择序。
在 NLP 领域，困惑度perplexity是评估语言模型预测标记序列的有效性的关键指标。在我们的分析范围内，“灵敏度”是指在模型分解后在校准数据集中观察到的困惑度的降低值。

这个sensitivity evaluation本质上就是探索神经网络对于不同截断的反应。定义了一个潜在的截断率$R=\{0.1,0.2,0.3,\cdots,0.9\}$，这些比率决定了截断SVD中为$m\times n$的权重矩阵保留的k秩的fraction，

$$r=\frac{km+kn}{mn}, r\in R$$

对LLM中的每个linear layer，迭代所有的ratio，对layer的权重矩阵进行截断SVD并替换为分解后的评估矩阵，对前面给出的calibration dataset评估其perplexity，这个迭代过程找到最优ratio来平衡模型压缩和评估误差下降。

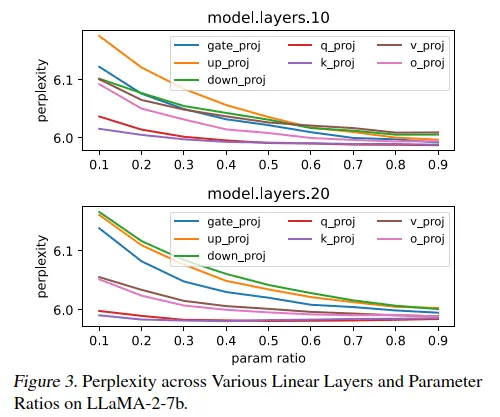
如图 3 所示，网络不同层之间的灵敏度存在明显差异。从这一分析中得出三个关键观察结果：

1. 相反比例关系：我们观察到困惑度与参数比率成反比。具体说来较低的参数比率往往会导致较高的困惑度分数。这一发现凸显了模型压缩和推理性能之间的关键权衡，表明仔细选择参数以保持平衡的重要性。
2. MLP 层中的更高灵敏度：多层感知器 （MLP） 中的层与前馈模块相比，表现出更高的灵敏度。这种区别对于指导压缩策略至关重要，表明在哪些地方需要更谨慎的截断。
3. 可变灵敏度层：某些层表现出相对较低的灵敏度，表明有可能在不显著性能下降的情况下进行更激进的压缩。这种变化表明 LLM 中存在冗余，为更有效的压缩方法提供了机会。针对这些不太敏感的层可以产生既紧凑又计算高效的模型。

评估敏感度后，编制了一个元组列表(layer, truncation rank, sensitivity),然后根据 sensitivity进行排序。设计了一个binary search algorithm，该算法旨在根据每层的灵敏度和对整体模型性能的贡献，来应对为每一层选择最有效截断等级的复杂性。

absorbing singular values

将$\Sigma$这个对角线融入其他的两个奇异值向量

$$W\approx U_k\Sigma_kV^T_k=U_k\sqrt{\Sigma_k}\cdot \sqrt{\Sigma_k}V_k^T=A_k\cdot B_k$$

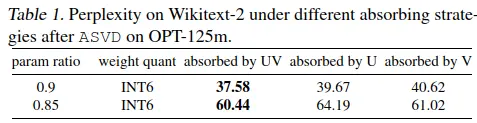
这个图与仅将奇异值Σk融合到U或V矩阵中的方法相比，我们提出的融合技术在权重量化方面具有显着优势
这确保了 Ak 和 Bk 的分布更加均匀，从而减少了不同通道之间的差异并减少了量化误差

Experimental Design and Results

hyper-parameters exploration

探索了前文提到的scaling matrix $S$的两种方法。

工具：OPT-125m

方法：在相对较小的网络OPT-125m上测试，测试$\alpha={0.1,0.25,0.5,1,2}$的影响。对于两种$S$的计算，将truncation ratio设置为0.9，使用binary search进行截断排名。将这两种指标进行两两组合计算在Wikitext2的测试集上的perplexity.

结论：根据谁的perplexity的最小值，与标准SVD STRS相比，两种激活感知方法都显示出更好的性能，$\alpha$取中值0.5最合适，且绝对平均值优于绝对最大值

evaluation of asvd on LLaMA models

工具：LLaMA-7b LLaMA-2-7b,每个都包含了7billion paramaters.对于每个模型，我们从维基文本数据集中选择了 32 个校准数据集，每个数据集包含 2048 个标记，以评估逐层灵敏度。

方法：设置不同的阈值 binary searching process，使我们能够观察不同压缩级别对模型性能的影响。该方法产生了一系列压缩网络，每个网络都具有独特的压缩比。我们使用困惑度作为主要指标来评估这些压缩网络的性能，重点关注两个数据集：Wikitext-2和Penn Treebank（PTB）。

结论：

• 随着参数比率的降低，困惑度相应增加。压缩的参数越多，SVD 引入的误差就越大。这会降低网络的表示能力，从而导致更高的困惑度分数。
• 当参数比值超过0.9时，观察到一个平台区域。在此范围内，ASVD 主要解压缩不太敏感的层，从而对预测准确性的影响最小。（
• 参数比值低于0.85时，困惑度迅速增加，表示更敏感的层正在被解压缩到较低的截断等级，从而对模型的性能产生不利影响。

integration ASVD with Quantization

如何将 ASVD 与量化技术集成以压缩大型语言模型，作为初步步骤，我们研究了 ASVD 与简单量化方法 RoundTo-Nearest （RTN） 和 4 位 NormalFloat （NF4）之间的协同作用。

方法：应用ASVD来分解网络，随后对分解的权重进行量化。我们采用每通道非对称量化，针对两个量化级别：8 位和 6 位。我们使用NF4来量化 4-bit。

在LLaMA-7b和LLaMA-2-7b上进行实验
进行了以下观察：

• 8 位量化：结果表明，8 位量化对原始网络和 ASVD压缩网络的模型性能影响可以忽略不计。
• 6 位量化：使用 6 位量化时，预测精度略有下降。这种效应在具有较高压缩率（较低参数比）的网络中更为明显，表明压缩和较低位量化的复合影响。
• 4 位量化：将网络量化为 NF4 后，观察到预测准确性进一步恶化。当参数比大于0.9时，量化导致的性能下降与非分解网络的性能下降基本一致。例如，在未分解的LLaMA-2-7b的情况下，NF4量化导致wiki PPL与FP16相比降低了0.18。同样，在参数比率0.95，NF4 定量产生的 PPL 与 FP16 相比降低了 0.19。
• 总之，研究结果表明ASVD与权重量化技术兼容。

decomposed network analysis

工具：在LLaMA-2-7a上使用ASVD压缩后，per-type parameters ratio and per-block parameters ratio随着params ratio的变化情况，

结论：

• 在MLP层中(gate projection, up projection and down projection)，参数有最好的压缩效果
• 在MHA层中，V projection layer的压缩相对小勺，而q projection layer和k projection layer可以显著被压缩
• 在per-block ratio中，第一层可以承受实质性的压缩。相比之下，除两个中间层外，其他层的压缩比，显示相似的压缩率。

Comparative Analysis

LQ-LoRA: Low-rank Plus Quantized Matrix Decomposition for Efficient Language Model Finetuning

• 我们提出了一种简单的方法，用于对预训练的语言模型进行内存高效调整。
• 我们的方法使用迭代算法将每个预训练矩阵分解为 a high-precision low-rank component and a memory-efficient quantized component。在微调期间，量化分量保持不变，仅更新低秩分量。我们提出了一个量化组件的整数线性规划公式，该公式可以在给定总体目标内存预算的情况下为每个矩阵动态配置量化参数（例如，位宽、块大小）。
• 我们进一步探索了该算法的数据感知版本，该算法使用Fisher信息矩阵的近似值在矩阵分解过程中对重建目标进行加权。
• 对 RoBERTa 和 LLaMA-2（7B 和 70B）进行调整的实验表明，我们的低秩加量化矩阵分解方法 （LQ-LoRA） 优于强大的 QLoRA 和 GPTQ-LoRA 基线，并且能够实现更积极的量化。例如，在 OpenAssistant 基准测试中，LQ-LoRA 能够学习 2.5 位 LLaMA-2 模型，该模型与使用 4 位 QLoRA 微调的模型竞争。在语言建模校准数据集上进行微调时，LQ-LoRA也可用于模型压缩;在此设置中，我们的 2.75 位LLaMA-2-70B 型号（包括低rank组件时平均为 2.85 位，需要 27GB GPU 内存）在全精度方面与origin model竞争。
• 这项工作提出了 LoRA 的简单扩展，它将预训练矩阵分解为低秩和量化组件，其中量化组件可以采用动态配置策略。我们观察到这种低秩加量化分解方法在语言建模中给定的量化水平上，对强基线产生了有意义的改进，指令调优和 GLUE 基准测试。
  模型微调：全面微调不合理，现有的可以根据数据在instruction上进行supervised finetuning。

HEAT: Hardware-Efficient Automatic Tensor Decomposition for Transformer Compression

• Transformer 在自然语言处理和计算机视觉方面取得了卓越的性能。它们的自注意力层和前馈层被过度参数化，限制了推理速度和能源效率。
• 张量分解是一种很有前途的技术，它通过利用张量代数属性以分解形式表达参数来减少参数冗余。以前的工作使用手动或启发式分解设置，而没有硬件感知定制，导致硬件效率低下和性能大幅下降。
• 在这项工作中，我们提出了一个硬件感知的张量分解框架，被称为 HEAT，能够有效地探索可能分解的指数空间，并通过硬件感知的协同优化自动选择张量化形状和分解等级。我们共同研究了张量收缩路径优化和融合的 Einsum 映射策略，以弥合理论优势与实际硬件效率提高之间的差距。我们的两阶段知识蒸馏流程解决了可训练性瓶颈，从而显着提高了分解变压器的最终精度。
• 总体而言，我们通过实验表明，与手动调整和启发式基线相比，我们的硬件感知分比式 BERT 变体将能量延迟积降低了 5.7× 的精度损失小于 1.1\%，并实现了更好的效率精度的Pareto frontier
• 在这项工作中，我们探索了硬件高效张量分解的大设计空间，并提出了用于 Transformer 模型压缩的自动分解框架 HEAT。我们超越了传统的手动分解，只关注压缩比或计算。
  我们在优化循环中考虑硬件成本，并有效地找到富有表现力和硬件效率的张量化形状。我们基于 SuperNet 的一次性排名搜索流程可以有效地生成优化的每张量分解排名设置。我们采用两级蒸馏流程来解决分解变压器的可训练性瓶颈，并显著提高其任务性能。
  实验表明，HEAT在我们定制的加速器上减少了高达5.7×的能量延迟积，精度下降小于1.1%。与手动和启发式张量分解方法相比，
  我们搜索的 HEAT 变体显示精度提高了 1-3%，硬件成本平均降低了 ∼30%。

Discussion and Limitations

Conclusion

% ## Title and Authors

% ## Background and Motivation

% ## Main Contributions

% ## Theoretical Framework/Algorithm

% ## Experimental Design and Results

% ## Comparative Analysis

% ## Discussion and Limitations

% ## Conclusion