Paper Analysis: Speeding-up Convolutional Neural Networks Using Fine-tuned CP-Decomposition

Title and Authors

• Title : Speeding-up Convolutional Neural Networks Using Fine-tuned CP-Decomposition
• Year: 2015
• Publication: ICLR

Background and Motivation

对于low-end architecture和real-time操作而言，减少CNN计算开销是必要的。而CNN中耗时最大的就是卷积层，提高卷积操作的效率是本文的目标。张量分解作为一种常见的加速卷积层的操作很常见。CNN中的典型卷积是将一个输入的3d张量（two spatial dimensions and one input image maps dimension）经过卷积计算得到一个相似结构的输出3d张量。而卷积核convolution kernel本身是一个4d张量（two spatial dimensions, one input image maps and output image maps dimension）.

Main Contributions

• 易于分解实现。CP分解具有很好理解的性质和成熟的实现
• 易于实现CNN。CP分解通过具有小的矩阵序列来近似4d核张量的卷积操作。所有的这些低维卷积都代表标准的CNN层，很容易使用现有的CNN包插入CNN中。
• 易于微调。一旦卷积层被替换为小矩阵序列，就可以直接使用反向传播对训练数据进行微调整个网络。
• 效率。与之前的方法相比the full kernel CPD和global 微调的简单组合可以为近似网络带来对于速度和准确度之间更好的均衡。

Theoretical Framework/Algorithm

方法可以总结为两步

1. 对卷积层中的卷积核使用张量分解。
2. 使用反向传播微调整个网络。

本文使用tenorlab中的non-linear least squares method来最小化估计残差的L2范数，使用Gauss-Newton优化。

现有generalized convolution，将input tensor $U(\cdot,\cdot,\cdot)\in\mathbb{R}^{X\times Y\times S}$映射到output tensor $V(\cdot,\cdot,\cdot)\in\mathbb{R}^{(X-d+1)\times (Y-d+1)\times T}$

$$V(x,y,t)=\sum_{i=x-\delta}^{x+\delta}\sum_{j=y-\delta}^{y+\delta}\sum_{s=1}^{S}K(i-x+\delta, j-y+\delta,s,t)U(i,j,s)$$

这里$K(\cdot,\cdot,\cdot,\cdot)$是一个4d核张量大小为$d{\times}d{\times}S{\times}T$ （the first two dimensions corresponding to the spatial dimensions, the third dimension corresponding to different input channels, the fourth dimension corresponding to different output channels.） The spatial width and height of the kernel are denoted as $d$, while $\delta$ denotes ``half-width’’ $(d-1)/2$ (for simplicity we assume square shaped kernels and even $d$).

The rank-$R$ CP-decomposition of the 4D kernel tensor has the form:

$$K(i,j,s,t) = \sum_{r=1}^R K^x(i-x+\delta,r) K^y(j-y+\delta,r)\\ K^s(s,r) K^t(t,r)$$

where $K^x(\cdot,\cdot)$, $K^y(\cdot,\cdot)$, $K^s(\cdot,\cdot)$, $K^t(\cdot,\cdot)$ are the four components of the composition representing 2D tensors (matrices) of sizes $d{\times}R$, $d{\times}R$, $S{\times}R$, and $T{\times}R$ respectively.

将上面两个公式结合，得到

$$V(x,y,t) = \sum_{r=1}^{R} K^t(t,r) \left(\sum_{i=x-\delta}^{x+\delta} K^x(i-x+\delta,r) \left(\sum_{j=y-\delta}^{y+\delta} K^y(j-y+\delta,r) \left(\sum_{s=1}^S \, K^s(s,r) \, U(i,j,s)\right)\right)\right)$$

此时，输出张量$V$可以通过4次使用更小的卷积核来进行卷积计算得到

$$\begin{align} U^s(i,j,r) &=\, \sum_{s=1}^S K^s(s,r)\, U(i,j,s) \tag{6}\\ U^{sy}(i,y,r) &= \sum_{j=y-\delta}^{y+\delta} K^y(j-y+\delta,r) \, U^s(i,j,r) \tag{7}\\ U^{syx}(x,y,r) &= \sum_{i=x-\delta}^{x+\delta} K^x(i-x+\delta,r) \, U^{sy}(i,y,r) \tag{8}\\ V(x,y,t) &= \sum_{r=1}^{R} K^t(t,r)\, U^{syx}(x,y,r)\,, \tag{9} \end{align}$$

其中 $U^s(\cdot,\cdot,\cdot)$, $U^{sy}(\cdot,\cdot,\cdot)$, and $U^{syx}(\cdot,\cdot,\cdot)$ are intermediate tensors (map stacks).

• 根据$U(\cdot,\cdot,\cdot)$计算 $U^s(\cdot,\cdot,\cdot)$（ Eq.$(6)$ ）以及根据 $U^{syx}(\cdot,\cdot,\cdot)$ 计算 $V(\cdot,\cdot,\cdot)$ ( Eq.$(9)$ )被称为 $1{\times}1$ convolutions。
• 根据$U^s(\cdot,\cdot,\cdot)$计算 $U^{sy}(\cdot,\cdot,\cdot)$ （ Eq.$(7)$ ）以及根据 $U^{sy}(\cdot,\cdot,\cdot)$ 计算 $U^{syx}(\cdot,\cdot,\cdot)$ （ Eq.$(8)$ ）是使用更小卷积核的标准卷积。
• 通过对训练数据进行标准反向传播（带动量）对生成的架构进行微调。所有网络层，包括近似层上方的层、近似层下方的层以及插入的四个卷积层都参与微调。然而，我们发现插入层内的梯度容易出现梯度爆炸，因此应该小心保持较低的学习率，或者修复部分或全部插入的层，同时仍然对上方和下方的层进行微调。

1. 点卷积（pointwise convolution）
   点卷积是一种特殊的卷积运算，他的卷积大小是$1 \times 1$。其作用主要是改变输入数据的通道数channels，在深度学习中用于将高维空间映射到地位空间，而不改变数据的空间维度（宽度和高度）

Experimental Design and Results

本文在两个network architecture上进行实验。

character-classification CNN

network由4个卷积层with maxout nonlinearities 以及 a softmax output，用来分类$24\times 24$ image patches为36 classes。我们只考虑第二层和第三层的卷积层，这两层占比时间超过90%。Layer 2有48 input 和 128 output channels以及大小为$9\times 9$，Layer 3有64 input 和 512 output channels以及大小为 $8\times 8$.

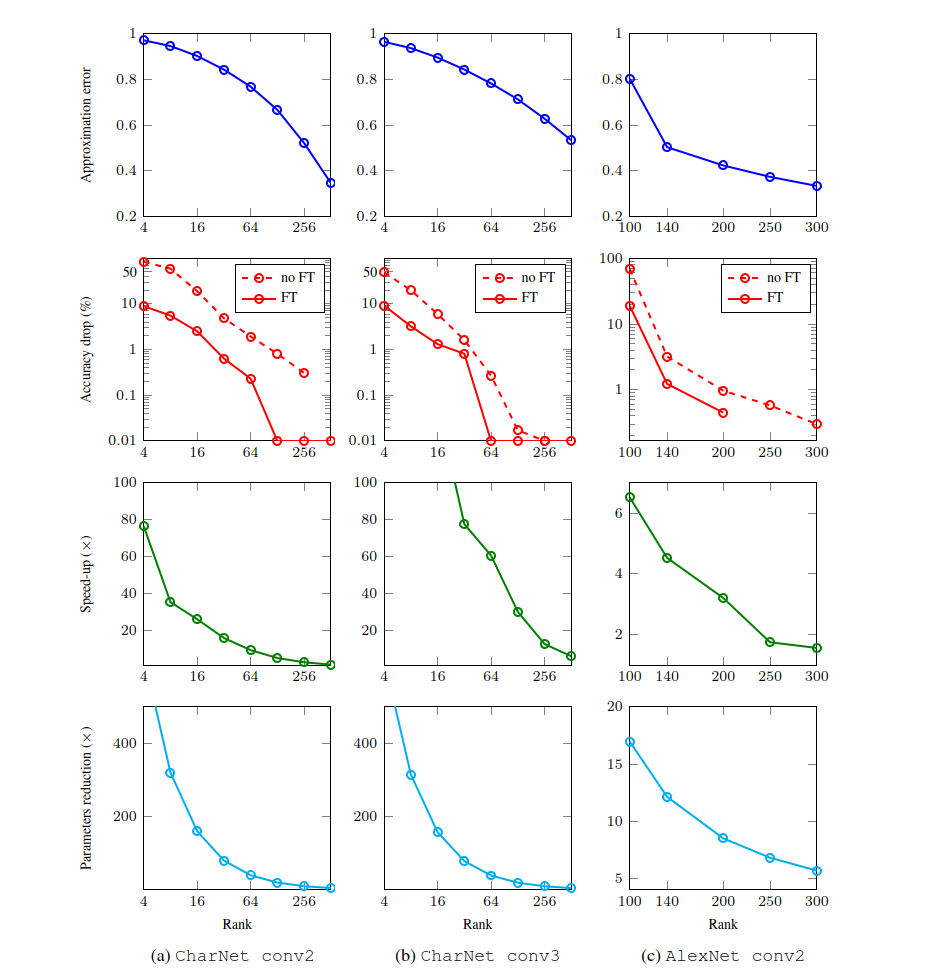
separate approximation.
张量近似误差随着近似秩的增加而减小，当近似秩变得足够大时，可以准确地近似权重张量。
然而，我们的实验表明，网络正常运行并不需要精确的近似。

combining approximations.
第 2 层近似于秩 64。在那之后，通过微调除新层之外的所有层，精度的下降很小。
最后，第 3 层以秩 64 近似，对于该层，这种近似不会导致网络预测精度显着下降，因此无需再次对网络进行微调。

此过程得出的网络比原始模型快 8.5 倍，而分类准确率下降 1% 至 90.2%

AlexNet

本文考虑了Alexnet的第二个卷积
可以注意到，所考虑网络的 conv2 需要更大的 rank （与
CharNetexperiment）来实现适当的性能。秩越大，精度损失越低，但模型加速比会降低。我们未能找到良好的SGD学习率：较大的值导致梯度爆炸，而较小的值则无法合理地减少重建损失。我们怀疑这种效应是由于低秩CP分解的不稳定性，规避这种问题的方法是使用交替更新因子矩阵。
虽然我们的方法在较小的架构（如字符分类）中更胜一筹，但对于像AlexNet这样的大型网络来说，它并不是最好的方法。

Comparative Analysis

Speeding-up and compression convolutional neural networks by low-rank decomposition without fine-tuning

• 背景：随着卷积神经网络（CNN）的快速发展，CNN的精度得到了显著提高，这也给资源有限的移动终端或嵌入式设备的部署带来了极大的挑战。最近，通过低秩分解压缩CNN取得了重大成就。
• 与现有方法使用相同的分解形式和基于奇异值分解（SVD）的分解策略进行微调不同，我们的方法对不同的层使用不同的分解形式，并提出了无需微调的分解策略。
• 我们提出了一种简单有效的方案来压缩整个CNN，称为余弦相似度SVD，无需微调。
• 对于AlexNet，与贝叶斯优化（BayesOpt）算法相比，我们的余弦相似度算法的秩选择需要84%的时间来找到秩。
• 在不同数据集上测试了各种CNN（AlexNet、VGG-16、VGG-19和ResNet-50）后，实验结果表明，当精度损失小于1%时，权重参数下降可以超过50%，而无需微调。浮点运算 （FLOP） 下降约为 20%，在不进行微调的情况下精度损失小于 1%。
  
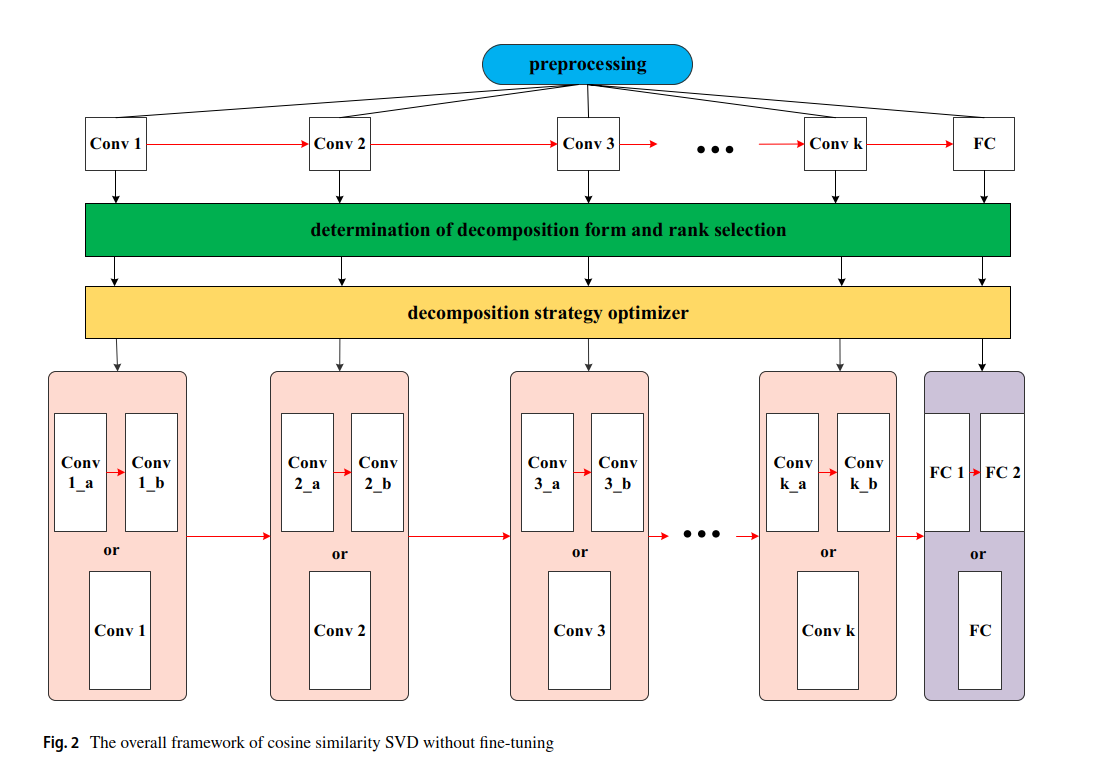
  拟议的方案由三部分组成，包括预处理、分解形式的测定和秩选择和分解策略优化。如上图所示，蓝色框表示预处理，其中包括读取预训练的 CNN参数。绿色框代表确定分解形式和秩选择，基于SVD对不同层使用不同的分解形式并通过我们的余弦相似度算法确定排名。黄色框表示分解策略优化器，无需微调来决定哪些层适合分解。底部框代表优化分解策略的最终结果。
  拟议的方案包括三个步骤。
  （1）需要对数据集进行CNN训练，并保存预训练参数，或直接读取预训练参数。
  （2）确定不同分解形式是关键并根据不同的层进行排名选择。我们自动排名算法适用于所有单排名解决方案。
  （3）通过我们的分解策略，无需微调，我们可以决定哪些层适合分解。分解策略没有微调避免了长时间的训练。
  

Deep Convolutional Neural Network Compression via Coupled Tensor Decomposition

• 背景：大型神经网络在各种现实世界的应用中取得了令人瞩目的进展。然而，运行深度网络需要昂贵的存储和计算资源，这使得它们在移动设备上部署时出现问题。
• 最近，矩阵和张量分解已被用于压缩神经网络。在本文中，我们开发了一种用于网络优化的同时张量分解技术。
• 首先讨论共享网络结构。有时，不仅结构而且参数也被共享以形成压缩模型，但代价是性能下降。这表明一个网络内各层之间的权重张量既包含相同的分量又包含独立的分量。
• 为了利用这一特性，针对完全和部分结构共享的情况开发了两种新的耦合张量序列分解，并提出了一种用于低秩张量计算的交替优化方法。
• 最后，我们通过微调来恢复神经网络模型的性能。然后可以计算所设计方法的压缩比。还包括实验结果，以证明我们的算法对于图像重建和分类应用的好处，使用众所周知的数据集，例如 Cifar-10/Cifar-100 和ImageNet 和广泛使用的网络，例如 ResNet。与最先进的基于独立矩阵和张量分解的方法相比，我们的模型可以在相同的压缩比下获得更好的网络性能

Discussion and Limitations

Conclusion