DNN的入门

Deep Neural Networks

DNN是一类执行分类、拟合和其它数据分析任务的模型。他们是由一系列的layer组成，每个layer在输入向量上执行线性或赋形变化，然后在生成的向量上应用非线性函数，称为激活函数。数据依次遍历这些层得到最终结果。执行其它功能的layer也可能出现在网络中，包含降低数据维度的pooling layer，提高网络对从未见过的数据性能的regularization layer。
神经网络中的数据和变化通常表示为tensor。网络在训练期间设置的值称为parameters或weights，将向网络呈现数据和更新参数的单一步骤称为一个training iteration。对所有训练数据集执行示例过程，直到网络得到充分训练，每次对整个训练数据集进行网络训练时，都被称为一个epoch。一个神经网络通常被训练上十或上百次。在训练过程中控制网络训练或操作但未被修改的值被称为hyperparameters.一旦网络被训练完成，参数就固定，模型可以用来分析新数据，这个过程称为inference。

最简单的神经网络layer是dense或fully-connected layer。密集层输入长度为的向量,产生长度为的向量，其参数由权重矩阵，他的实现函数为$y=f(Wx+b)$其中是activation function。深度神经网络在输入和输出之间具有许多层，使它们能够学习非常复杂的函数，并减少或消除对特征提取的需求。与其他统计模型相比，DNN 具有非常多的参数，通常从数十万到数亿个参数不等。

现代DNN在根据其训练数据进行评估时通常可以达到非常高的准确性，但在未知数据集上获得类似性能可能会很大难度。已经开发了很多方法来改善未知数据集的模型性能，有时以降低训练数据的性能为代价，这些方法称为regularization。它们包括对训练过程的修改、对优化器目标的修改以及神经网络中的其他层，例如 dropout和batch normalization层。

接下来是详细描述，来源是刘建平的博客.

感知机到神经网络

感知机的模型如下，他是由若干输入和一个输出组成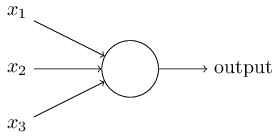

输入和输出学习到一个线性关系，得到中间的输出结果

$$z=\sum\limits_{i=1}^mw_ix_i + b$$

接着是一个神经元激活函数

$$sign(z)= \begin{cases} -1& {z<0}\\ 1& {z\geq 0} \end{cases}$$

神经网络在感知机的模型上做了扩展，总结如下有三点

1. 加入了隐藏层
   
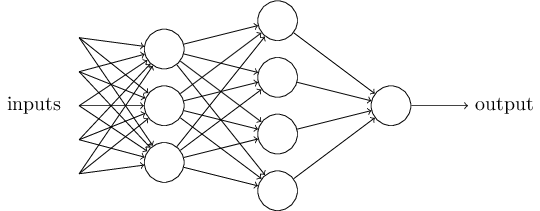
2. 输出层的神经元有多个
   
3. 激活函数的扩展

DNN的基本结构

DNN可以理解为有很多隐藏层的神经网络，DNN有时也被称为multi-layer perception, MLP.
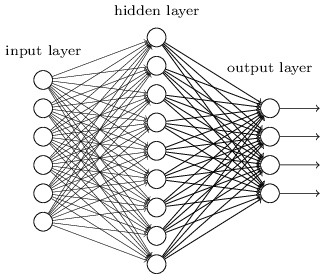
从DNN按不同层的位置划分，DNN内部的神经网络层可以分为三类，输入层，隐藏层和输出层。第一层是输入层，最后一层是输出层，而中间的层数是隐藏层。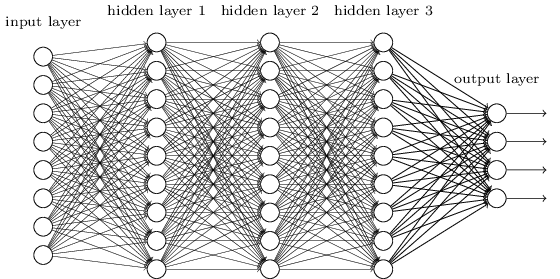

层与层之间是全连接的，也就是说第i层的任意一个神经元一定与第i+1层的任意一个神经元相连。
由于DNN的层数很多，因此参数有很多。

• 权重参数。第l-1层的第k个神经元到第l层的第j个神经元的权重参数定义为.注意，输入层没有参数。以下图三层的DNN为例，第二层的第4个神经元到第三层的第2个神经元的权重参数定义为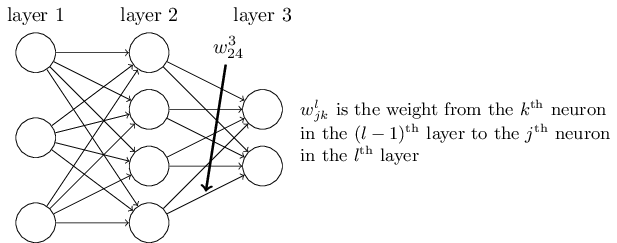
  
• 偏倚的定义。第二层的第三个神经元的偏倚定义为

DNN前向传播算法数学原理

假设我们选择的激活函数是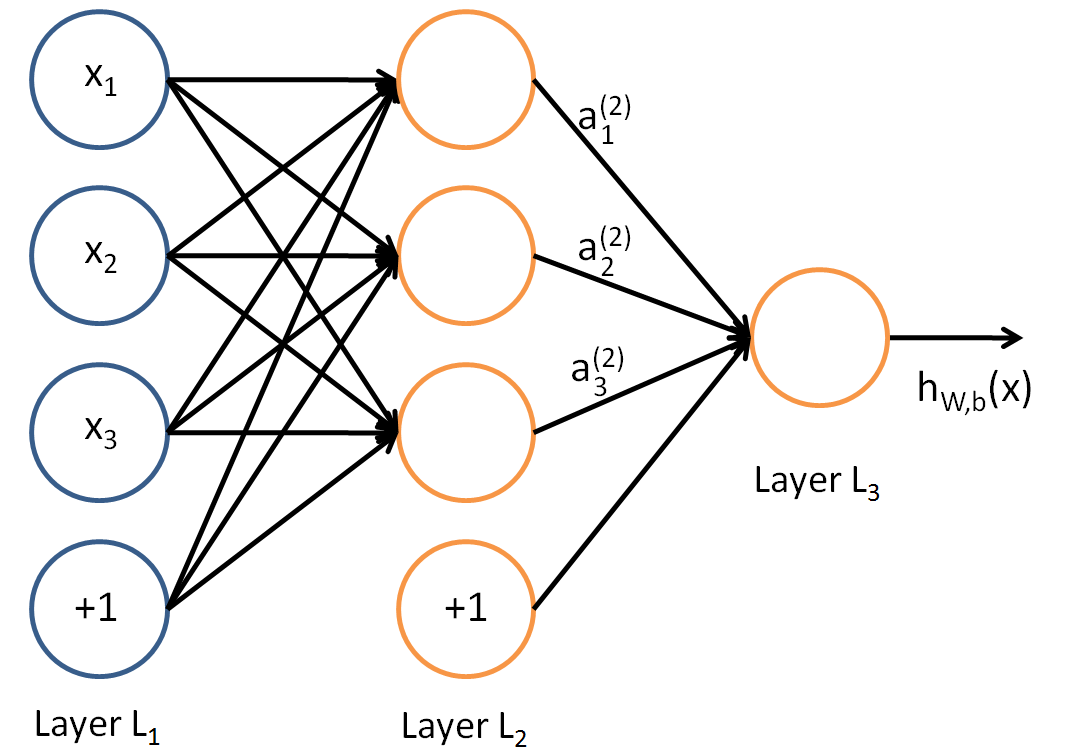，隐藏层和输出层的输出值为，则对于下图的三层DNN，利用和感知机一样的思路，我们可以使用上一层的输出计算下一层的输出，就是DNN前向传播算法。

对于第二层的输出，我们有

$$a_1^2=\sigma(z_1^2) = \sigma(w_{11}^2x_1 + w_{12}^2x_2 + w_{13}^2x_3 + b_1^{2})\\ a_2^2=\sigma(z_2^2) = \sigma(w_{21}^2x_1 + w_{22}^2x_2 + w_{23}^2x_3 + b_2^{2})\\ a_3^2=\sigma(z_3^2) = \sigma(w_{31}^2x_1 + w_{32}^2x_2 + w_{33}^2x_3 + b_3^{2})$$

对于第三层的输出，有

$$a_3^1 =\sigma(z_3^1) = \sigma(w_{11}^3a_1^2 + w_{12}^3a_2^2 + w_{13}^3a_3^2 + b_1^{3})$$

假设第层共有m个神经元，则对于第个神经元的输出,我们有

$$a_j^l = \sigma(z_j^l) = \sigma(\sum\limits_{k=1}^mw_{jk}^la_k^{l-1} + b_j^l)$$

使用矩阵去描述的话就是会简洁很多。假设第层共有个神经元，而第层共有个神经元，则第层的权重系数组成看一个的矩阵，第层的偏倚组成了一个的向量，第层的输出组成了一个的向量，第层的未激活前的线性输出组成了一个的向量，第层的输出组成了一个的向量.用矩阵表示，第l层的输出为

$$a^l = \sigma(z^l) = \sigma(W^la^{l-1} + b^l)$$

DNN反向传播算法的基本思路

回到我们监督学习的一般问题，假设我们有 m 个训练样本：, 其中 为输入向量，特征维度为 , 而 为输出向量，特征维度为 。我们需要利用这 m 个样本训练出一个模型，当有一个新的测试样本 来到时, 我们可以预测 向量的输出。

如果我们采用 DNN 的模型，即我们使输入层有 个神经元，而输出层有 个神经元。再加上一些含有若干神经元的隐藏层。此时我们需要找到合适的所有隐藏层和输出层对应的线性系数矩阵 , 偏倚向量 , 让所有的训练样本输入计算出的输出尽可能的等于或很接近样本输出。
可以用一个合适的损失函数来度量训练样本的输出损失，接着对这个损失函数进行优化求最小化的极值，对应的一系列线性系数矩阵 , 偏倚向量 即为我们的最终结果。
对 DNN 的损失函数用梯度下降法进行迭代优化求极小值的过程即为我们的反向传播算法。

在进行 DNN 反向传播算法前，我们需要选择一个损失函数，来度量训练样本计算出的输出和真实的训练样本输出之间的损失。你也许会问：训练样本计算出的输出是怎么得来的？这 个输出是随机选择一系列 , 用我们上一节的前向传播算法计算出来的。即通过一系列的计算：。计算到输出层第 层对应的 即为前向传播算法计算出来的输出。

回到损失函数，DNN 可选择的损失函数有不少，为了专注算法，这里我们使用最常见的均方差来度量损失。即对于每个样本，我们期望最小化下式：

$$J(W,b,x,y) = \frac{1}{2}||a^L-y||_2^2$$

　　　　其中，和 为特征维度为 的向量, 而 为 S 的 L2 范数。

损失函数有了，现在我们开始用梯度下降法迭代求解每一层的 。首先是输出层第 层。注意到输出层的 满足下式：

$$a^L = \sigma(z^L) = \sigma(W^La^{L-1} + b^L)$$

这样对于输出层的参数，我们的损失函数变为：

$$J(W,b,x,y) = \frac{1}{2}||a^L-y||_2^2 = \frac{1}{2}|| \sigma(W^La^{L-1} + b^L)-y||_2^2$$

Sparsity

在DNN中

Neural Network Pruning

DNN中的大量参数使他们在实践中难以应用。neural network pruning属于最后一类。修剪方法是用于训练神经网络或调整已经训练过的网络的技术，以便其大量参数变为零。这样做的方式是尽量减少修剪导致的推理准确性的降低。如果我们将每个参数视为表示线性变换中输入和输出之间的连接，则可以将修剪视为删除这些连接。如下所示，pruning fraction或pruning rate是图层或网络中被修剪的connected fraction。

使用修剪来加速推理时，一个重要的问题是，所讨论的硬件是否可以实际利用修剪的表示形式。通常需要强加某种结构来管理可以修剪哪些连接，以便看到显着的改进。例如，这可能意味着删除权重矩阵的整行，而不是矩阵的任意元素。以需要遵循特定结构的方式修剪称为结构化修剪，而没有结构要求的修剪称为非结构化修剪。 使用结构化而不是非结构化修剪会带来权衡。粗略地说，结构越严格，可以删除的连接就越少，而不会严重损害网络的准确性。这是因为非结构化修剪可以更自由地删除那些对网络性能损害最小的权重。在实践中，决定是否使用结构化修剪以及如果是，要施加什么结构要求取决于特定应用程序的要求以及用于推理的硬件。

GPU设计准则

参考了文章

latency hiding with TLP and ILP

如果 GPU 上驻留了足够的warp（如果我们有足够的 TLP），则在warp之间切换可以完全隐藏长延时操作的成本。我们将程序中的 TLP 数量量化为占用率occupancy，即可用（发出的）warp与 GPU 可支持的最大warp数之比。更高的占用率产生更好的延迟隐藏能力，这使我们能够实现充分利用。
另一种延迟隐藏策略是利用指令级并行性（ILP）及其利用单个线程中多个内存操作的延迟重叠的能力。由于 GPU 的内存系统是深度流水线的，因此线程在变为非活动状态之前可能会发出多个独立的长延迟操作，并且这些多个操作将共同产生与单个操作大致相同的延迟。虽然这产生了显著的性能优势，但它依赖于程序员向硬件公开独立的内存操作。我们可以通过将多个独立任务分配给同一线程（“线程粗化”）来实现此目标。

GPU 具有固定数量的寄存器。TLP 需要许多驻留warp，每个warp都需要寄存器。ILP 会增加每个线程的工作，因此每个线程需要更多的寄存器。因此，TLP和ILP是对立的，要充分利用这两种技术，就需要仔细平衡这两种技术。虽然TLP通常用于所有GPU计算，但ILP是一个较少探索的领域。

load-balancing

我们现在转向的问题是，确保所有计算单元在每个周期上都做有用的工作，并且从这些warp访问的内存被合并以确保峰值内存性能。在SpMV和SpMM的content中，这种“负载平衡”问题有两个方面：

1. warp之间的负载不均。某些 CTA(block) 或 warp 分配的工作量可能比其他 CTA 或 warp 少，这可能导致这些负载较少的计算单元处于空闲状态，而负载较多的计算单元继续执行有用的工作。在本文中，我们称之为“Type 1”负载不平衡。
2. warp内部的负载不均。在两个方面，我们统称为“Type 2”负载不平衡。
   (a) 某些warp可能没有足够的work来占用warp中的所有32个线程。在这种情况下，线程单元处于空闲状态，我们会损失性能。
   (b) 某些warp可能会将不同的任务分配给不同的线程。 在这种情况下，线程内的 SIMT 执行意味着某些线程处于空闲状态，而其他线程正在运行;此外，执行过程中的warp分化意味着整个warp中的内存访问不太可能合并。